Основные формулы тригонометрии

Содержание

Определения синуса, косинуса, тангенса и котангенса угла
Основное тригонометрическое тождество
Зависимость между синусом, косинусом, тангенсом и котангенсом
Чётность, нечётность и периодичность тригонометрических функций
Формулы сложения
Формулы двойного и тройного аргумента
Формулы понижения степени
Формулы приведения
Формулы суммы и разности синусов
Формулы суммы и разности косинусов
Формулы суммы и разности тангенсов
Преобразование произведения синусов и косинусов в сумму (разность)
Выражение синуса и косинуса через тангенс половинного аргумента

Определения синуса, косинуса, тангенса и котангенса угла.

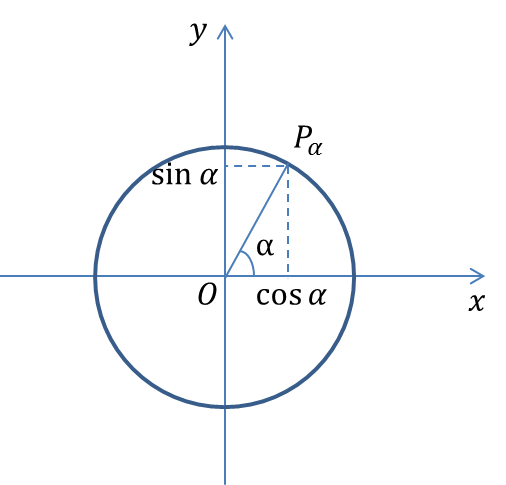
Синус угла $\alpha$ (обозначается $\sin\alpha$ ) – ордината точки $P_{\alpha},$ полученной поворотом точки $P(1; 0)$ вокруг начала координат на угол $\alpha.$

Косинус угла $\alpha$ (обозначается $\cos\alpha$ ) – абсцисса точки $P_{\alpha},$ полученной поворотом точки $P(1; 0)$ вокруг начала координат на угол $\alpha.$

Тангенс угла $\alpha$ (обозначается $\operatorname{tg}\alpha$ ) – отношение синуса угла $\alpha$ к его косинусу, то есть

$\operatorname{tg}\alpha = \frac{\sin\alpha}{\cos\alpha}.$

Котангенс угла $\alpha$ (обозначается $\operatorname{ctg}\alpha$ ) – отношение косинуса угла $\alpha$ к его синусу, то есть

$\operatorname{ctg}\alpha = \frac{\cos\alpha}{\sin\alpha}.$

Основное тригонометрическое тождество

$\sin^2\alpha + \cos^2\alpha = 1.$

Зависимость между синусом, косинусом, тангенсом и котангенсом

$\operatorname{tg}\alpha\operatorname{ctg}\alpha = 1,$

$1 + \operatorname{tg}^2\alpha = \frac{1}{\cos^2\alpha},$

$1 + \operatorname{ctg}^2\alpha = \frac{1}{\sin^2\alpha}.$

Чётность, нечётность и периодичность тригонометрических функций.

Косинус – чётная функция, а синус, тангенс и котангенс – нечётные функции аргумента $\alpha$ :

$\cos(-\alpha) = \cos\alpha,$

$\sin(-\alpha) = -\sin\alpha,$

$\operatorname{tg}(-\alpha) = -\operatorname{tg}\alpha,$

$\operatorname{ctg}(-\alpha) = -\operatorname{ctg}\alpha.$

Синус и косинус – периодические с периодом $2\pi$ функции, а тангенс и котангенс – периодические с периодом $\pi$ функции:

$\sin(\alpha + 2\pi) = \sin\alpha,$

$\cos(\alpha + 2\pi) = \cos\alpha,$

$\operatorname{tg}(\alpha + \pi) = \operatorname{tg}\alpha,$

$\operatorname{ctg}(\alpha + \pi) = \operatorname{ctg}\alpha.$

Число $2\pi$ является наименьшим положительным периодом синуса и косинуса, а число $\pi$ – наименьшим положительным периодом тангенса и котангенса.

Для любого целого $n$ справедливы равенства

$\sin(\alpha + 2\pi n) = \sin\alpha,$

$\cos(\alpha + 2\pi n) = \cos\alpha,$

$\operatorname{tg}(\alpha + \pi n) = \operatorname{tg}\alpha,$

$\operatorname{ctg}(\alpha + \pi n) = \operatorname{ctg}\alpha.$

Формулы сложения

$\sin(\alpha + \beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta,$

$\sin(\alpha - \beta) = \sin\alpha\cos\beta - \cos\alpha\sin\beta,$

$\cos(\alpha + \beta) = \cos\alpha\cos\beta - \sin\alpha\sin\beta,$

$\cos(\alpha - \beta) = \cos\alpha\cos\beta + \sin\alpha\sin\beta,$

$\operatorname{tg}(\alpha + \beta) = \frac{\operatorname{tg}\alpha + \operatorname{tg}\beta}{1 - \operatorname{tg}\alpha\operatorname{tg}\beta},$

$\operatorname{tg}(\alpha - \beta) = \frac{\operatorname{tg}\alpha - \operatorname{tg}\beta}{1 + \operatorname{tg}\alpha\operatorname{tg}\beta}.$

Формулы двойного и тройного аргумента

$\sin{2\alpha} = 2\sin{\alpha}\cos{\alpha},$

$\cos{2\alpha} = \cos^2{\alpha} - \sin^2{\alpha} = 2\cos^2{\alpha}-1 =1 - 2 \sin^2{\alpha},$

$\operatorname{tg}2\alpha = \frac{2\operatorname{tg}\alpha}{1- \operatorname{tg} ^2{\alpha}},$

$\sin 3\alpha = 3\sin\alpha - 4\sin^3{\alpha},$

$\cos 3\alpha = 4\cos^3\alpha - 3\cos{\alpha},$

$\operatorname{tg}3\alpha=\frac{3\operatorname{tg}\alpha - \operatorname{tg}^3\alpha}{1 - 3\operatorname{tg}^2\alpha}.$

Формулы понижения степени

$\cos^2\alpha = \frac{1 + \cos 2\alpha}{2},$

$\sin^2\alpha = \frac{1 - \cos 2\alpha}{2}.$

Формулы приведения

$\sin\left(\frac{\pi}{2}-\alpha\right)=\cos\alpha,\qquad\sin\left(\frac{\pi}{2}+\alpha\right)=\cos\alpha,$

$\sin\left(\pi-\alpha\right)=\sin\alpha,\qquad\sin\left(\pi+\alpha\right)=-\sin\alpha,$

$\cos\left(\frac{\pi}{2}-\alpha\right)=\sin\alpha,\qquad\cos\left(\frac{\pi}{2}+\alpha\right)=-\sin\alpha,$

$\cos\left(\pi-\alpha\right)=-\cos\alpha,\qquad\cos\left(\pi+\alpha\right)=-\cos\alpha.$

Формулы суммы и разности синусов

$\sin\alpha + \sin\beta = 2\sin\frac{\alpha + \beta}{2}\cos\frac{\alpha - \beta}{2},$

$\sin\alpha - \sin\beta = 2\sin\frac{\alpha - \beta}{2}\cos\frac{\alpha + \beta}{2}.$

Формулы суммы и разности косинусов

$\cos\alpha + \cos\beta = 2\cos\frac{\alpha + \beta}{2}\cos\frac{\alpha - \beta}{2},$

$\cos\alpha - \cos\beta = -2\sin\frac{\alpha + \beta}{2}\sin\frac{\alpha - \beta}{2}.$

Формулы суммы и разности тангенсов

$\operatorname{tg}\alpha + \operatorname{tg}\beta = \frac{\sin(\alpha + \beta)}{\cos\alpha\cos\beta},$

$\operatorname{tg}\alpha - \operatorname{tg}\beta = \frac{\sin(\alpha - \beta)}{\cos\alpha\cos\beta}.$

Преобразование произведения синусов и косинусов в сумму (разность)

$\sin\alpha\cos\beta = \frac{\sin(\alpha + \beta) + \sin(\alpha - \beta)}{2},$

$\cos\alpha\cos\beta = \frac{\cos(\alpha + \beta) + \cos(\alpha - \beta)}{2},$

$\sin\alpha\sin\beta = \frac{\cos(\alpha - \beta) - \cos(\alpha + \beta)}{2}.$

Выражение синуса и косинуса через тангенс половинного аргумента

$\sin\alpha = \frac{2\operatorname{tg}\frac{\alpha}{2}}{1 + \operatorname{tg}^2\frac{\alpha}{2}},$

$\cos\alpha = \frac{1 - \operatorname{tg}^2\frac{\alpha}{2}}{1 + \operatorname{tg}^2\frac{\alpha}{2}}.$