Синус, косинус, тангенс и котангенс онлайн

( )

Градусы Радианы Грады

Определения синуса, косинуса, тангенса и котангенса

Синус угла $\alpha$ (обозначается $\sin\alpha$ ) – ордината точки $P_{\alpha}$ , полученной поворотом точки $P(1; 0)$ вокруг начала координат на угол $\alpha$ .

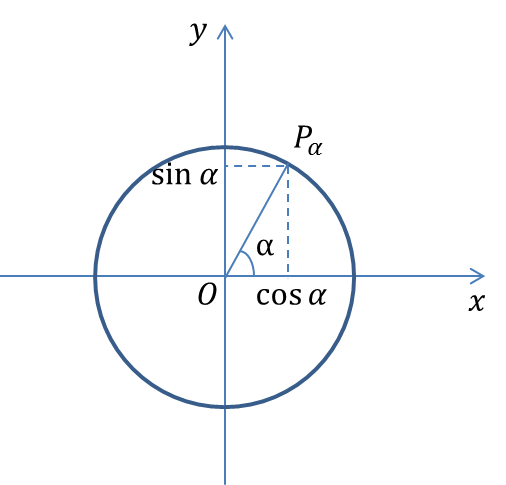
Косинус угла $\alpha$ (обозначается $\cos\alpha$ ) – абсцисса точки $P_{\alpha}$ , полученной поворотом точки $P(1; 0)$ вокруг начала координат на угол $\alpha$ .

Тангенс угла $\alpha$ (обозначается $\operatorname{tg}\alpha$ ) – отношение синуса угла $\alpha$ к его косинусу, то есть

$\operatorname{tg}\alpha = \frac{\sin\alpha}{\cos\alpha}.$

Котангенс угла $\alpha$ (обозначается $\operatorname{ctg}\alpha$ ) – отношение косинуса угла $\alpha$ к его синусу, то есть

$\operatorname{ctg}\alpha = \frac{\cos\alpha}{\sin\alpha}.$

Таблица значений синуса, косинуса, тангенса и котангенса

$\alpha$ , радианы	$0$	$\frac{\pi}{6}$	$\frac{\pi}{4}$	$\frac{\pi}{3}$	$\frac{\pi}{2}$
$\alpha$ , градусы	$0^{\circ}$	$30^{\circ}$	$45^{\circ}$	$60^{\circ}$	$90^{\circ}$
$\sin\alpha$	$0$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	$1$
$\cos\alpha$	$1$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	$0$
$\operatorname{tg}\alpha$	$0$	$\frac{1}{\sqrt{3}}$	$1$	$\sqrt{3}$	$-$
$\operatorname{ctg}\alpha$	$-$	$\sqrt{3}$	$1$	$\frac{1}{\sqrt{3}}$	$0$