Содержание
Уравнение прямой на плоскости
Уравнения прямой на плоскости в координатной форме
то есть числа одновременно не равны нулю.
где числа не равны нулю одновременно. Числа
являются компонентами направляющего вектора прямой — ненулевого вектора, лежащего на прямой.
При или
это уравнение принимает соответственно вид
или
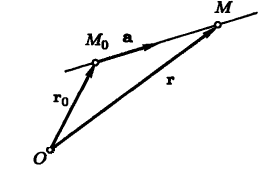
Уравнения прямой на плоскости в векторной форме
где — направляющий вектор прямой,
— радиус-вектор некоторой точки прямой.
Нормальное векторное уравнение прямой:
где — вектор нормали к прямой.
Это уравнение также можно записать в форме
причём если вектор — единичный, то величина
есть расстояние от точки
до прямой. Вообще говоря, это уравнение имеет следующий смысл: проекция радиус-вектора любой точки прямой на нормаль к этой прямой постоянна.
Векторное уравнение прямой, проходящей через две различные точки:
где и
— радиус-векторы данных точек.
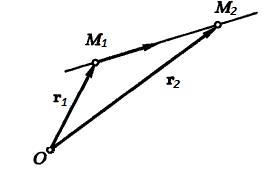
Это уравнение легко получается из векторного уравнения прямой в параметрической форме, если в качестве направляющего вектора прямой взять вектор
Уравнение прямой в пространстве
Уравнение прямой в пространстве в координатной форме
Числа являются компонентами направляющего вектора прямой.
Исключением параметра параметрические уравнения прямой приводятся к канонической форме:
Если, например, то канонические уравнения принимают вид
Аналогично для любой другой компоненты направляющего вектора.
Если два параметра равны нулю, например, то канонические уравнения имеют вид
Аналогично для любых других пар компонент направляющего вектора.
Уравнение прямой в пространстве, проходящей через две точки и
:
Если, например, то уравнения прямой принимают вид
Если к тому же то уравнения прямой записываются в виде
Аналогично для любых двух пар совпадающих координат точек.
Уравнение прямой в пространстве в векторной форме
где — направляющий вектор прямой,
— радиус-вектор некоторой точки прямой. Это уравнение совпадает с параметрическим векторным уравнением прямой на плоскости.

или
где и
— радиус-векторы двух точек прямой.
